2218. Maximum Value of K Coins From Piles | Daily Challange - 2023-04-15

2218. Maximum Value of K Coins From Piles - Hard

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

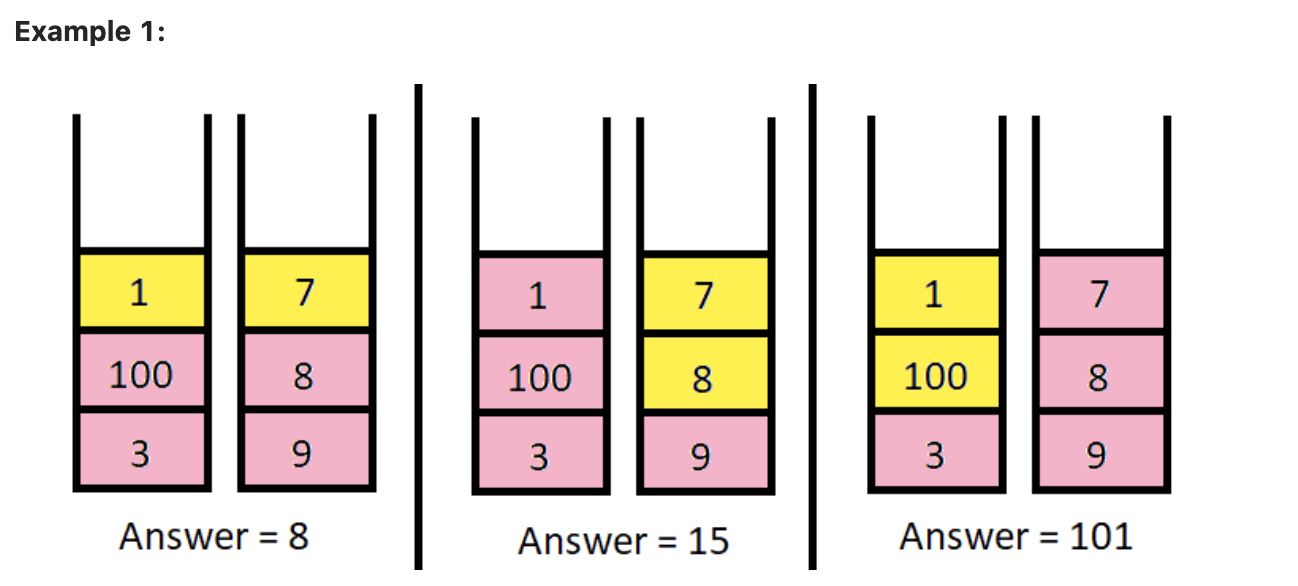
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example2 

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

n == piles.length
1 <= n <= 1000
1 <= piles[i][j] <= 105
1 <= k <= sum(piles[i].length) <= 2000

Java Solution

이 문제를 하위 문제로 분해하여 동적프로그램잉 방법으로 해결할 수 있습니다. 

첫번째 i 더미에서 j 개의 동전을 선택할 때의 최대 동적 가치를 저장하기 위해 2d 배열 DP[i][j]를 만들 수 있습니다. 

다음으로 배열을 반복하고 현재 더미에 모든 가능한 선택지를 시도하여 각 하위 문제의 최대 동전 가치를 계산하고 최대 결과를 업데이트 할 수 있습니다.

 

Complexity? 

시간복잡도 - O(n^3) -> 여기 n을 한 더미에서 최대 동전 수입니다.

공간복잡도 - O(nk) -> 우리 결과 데이터를 저장하기 위해 (n+1) x (k+1) 크기의 2차원 배열을 사용합니다.

 

class Solution {
    public int maxValueOfCoins(List<List<Integer>> piles, int k) {
        
        int[][] dp = new int[piles.size() + 1][k + 1];
        Arrays.fill(dp[0], 0);
        
        for (int i = 1; i <= piles.size(); i++) {
            dp[i][0] = 0;
        }
        
        for (int i = 1; i <= piles.size(); i++) {
            for (int j = 1; j <= k; j++) {
                int cur = 0;
                for (int x = 0; x < Math.min(piles.get(i - 1).size(), j); x++) {
                    cur += piles.get(i - 1).get(x);
                    dp[i][j] = Math.max(dp[i][j], cur + dp[i - 1][j - x - 1]);
                }
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
            }
        }
        return dp[piles.size()][k];
    }
}

실행 결과

 

Leetcode 문제 페이지