Insertion Algorith - 삽입 정렬

삽입 정렬은 카드 놀이를 할 때 손에 쥔 카드를 정렬하는 것과 방법이 같습니다.

왼손ㄴ은 비었고 카드가 탁자 위에 뒤집힌 채 쌓여 있다고 하자. 이제 탁자에서 카드를 한 장씩 가져와 왼손의 적절한 위치에 삽입합니다. 카드를 삽입할 적절한 위치를 찾기 위해 왼손에 이미 든 카드와 새 카드를 오른쪽ㅇ서 왼쪽에서 왼쪽 방향으로 차례로 비교하면 됩니다. 왼손에 있는 카드는 항상 정렬되어 있고, 이는 처음에 탁자에서 맨 위에 쌓였던 카드입니다.

입력: n개 수들의 수열(a1,a2,a3,a4...,an)

출력: a1<=a2<=a3<=a4...<=an 을 만족하는 입력 수열의 순열 (재배치) {a1,a2,a3,a4....,an}

---

배열 A = {5,1,8,3,9,2}에 대한 삽입 정렬의 수행 과정

1. 두 번째 자료인 1를 키로 해서 그 이전의 자료들과 비교한다.

  -> 키 값 1과 첫번째 자료인 5를 비교한다. 5 1보다 크므로 5를 1자리에 넣고 키 값 1을 5의 자리인 첫번째에 기억시킨다.

2. 세번째 자료인 8을 키 값으로 해서 그 이전의 자료들과 비교한다.

  -> 키 값 8과 두 번째 5를 비교한다. 5가 키 값보다 작으므로 그냥 넘어간다.

3. 네번째 3을 키 값으로 해서 그 이전의 자료와 비교한다.

  -> 키 값 3과 세 번째 자료인 8을 비교한다. 키 값보다 크므로 8을 3이 있던 네 번째 자리에 기억시킨다.

  -> 키 값 3와 세번째 두 번째 자료인 5를 비교한다. 키 값보다 크므로 5를 2가 있던 자리에 기억시킨다.

  -> 키 값 3와 첫번째 자료인 1을 비교한다. 키 값보다 작으므로 두 번째 자리에 기억시킨다.

4. 다섯번째 자료인 9을 키 값으로 해서 그 이전의 자료들과 비교한다.

  -> 키 값 9을 네 번째 자료인 8을 비교한다. 8일 키 값보다 작으므로 9을 다섯번째 자리에 기억시킨다.

5. 여섯번째 자료인 2를 키 값으로 해서 그 이전의 자료드과 비교한다.

  -> 키 값 2를 다섯번째 9을 비교한다. 9이 키 값보다 크므로 9을 2가 있던 자리에 기억시킨다.

  -> 키 값 2를 네 번째 8을 비교한다. 8이 키 값보다 크므로 8을 2가 있던 자리에 기억시킨다.

  -> 키 값 2를 세 번째 5를 비교한다. 5가 키 값보다 크므로 5를 2가 있던 자리에 기억시킨다.

  -> 키 값 2를 두 번째 3을 비교한다. 3이 키 값보다 크므로 3을 2가 있던 자리에 기억시킨다.

  -> 키 값 2를 첫 번째 1을 비교한다. 1을 키 값보다 작으므로 2를 두 번째 자리에 기억시킨다.

 

Insertion sort - 삽입 정렬 유스코드

오름차순

for j = 2 to A.length
	key = A[j]
    // A[j]를 정렬된 배열 A[1..j-1]에 삽입한다.
    i = j - 1
    while i > 0 그리고 A[i] > key
    	A[i+1] = A[i]
        i = i - 1
    A[i+1] = key

내림차순

for j = 2 to A.length
	key = A[j]
    // A[j]를 정렬된 배열 A[1..j-1]에 삽입한다.
    i = j - 1
    while i > 0 그리고 A[i] < key
    	A[i+1] = A[i]
        i = i - 1
    A[i+1] = key

 

자바 소스코드

public class InsertionSort {

    public static void main(String[] args) {
        int[] nums = { 5, 2, 4, 6, 1, 3 };
        System.out.print("List before -> : ");
        for (int i : nums) {
            System.out.print(i + ", ");
        }
        for (int j = 1; j < nums.length; j++) {
            int key = nums[j];
            int i = j - 1;
            while (i >= 0 && nums[i] < key) {
                nums[i + 1] = nums[i];
                i = i - 1;
            }
            nums[i + 1] = key;
        }
        System.out.println();
        System.out.print("Insertion Sort After Sorting -> ");
        for (int i : nums) {
            System.out.print(i + ", ");
        }
    }

}

결과 값 -> 

 

복잡도

n개의 데이터가 있을 때, 최악의 경우에는

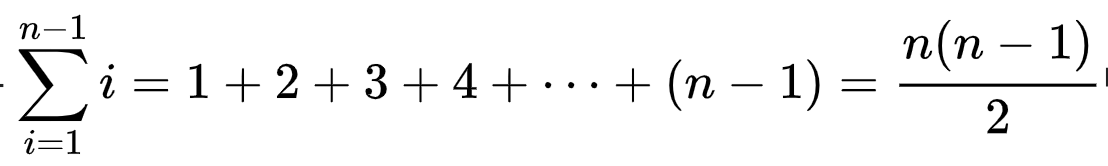
번의 비교를 하게 되므로,

최악 시간 복잡도는  -> O(n2) 비교 및 교환

최선 시간 복잡도는 -> O(n) 비교, O(1)교환

평균 시간 복잡도는 -> O(n2) 비교 및 교환

공간 복잡도 -> O(n) 전체, O(1) 보조